Aunque han pasado más de 20 años de su obtención en el laboratorio, todavía son frecuentes las noticias que aparecen acerca del descubrimiento de nuevas propiedades de este material , a veces un tanto exóticas e inesperadas.
Hace unas semanas atrás la página de Facebook “Astronomía y Cosmos” publicó una noticia con el titular “Los electrones del grafeno acaban de hacer algo que los físicos creían imposible”. También apareció una noticia con el mismo tema en el sitio web de divulgación científica Science Daily , en este caso titulada “Graphene just broke a fundamental law of physics” (“El grafeno acaba de violar una ley fundamental de la Física”).
Aunque los titulares tienen un tono un poco sensacionalista, están refiriéndose a resultados muy interesantes y dignos de atención. Se trata en particular de un trabajo experimental realizado por investigadores del Instituto Indio de Ciencias en Bangalore, India, en colaboración con científicos de Estados Unidos y Japón , expuesto en el número 21 de 2005 de la prestigiosa revista Nature Physics. En él, entre otros aspectos, se demuestra de manera rigurosa y fehaciente que en el grafeno, bajo determinadas circunstancias, se produce una violación gigante de la ley de Wiedemann-Franz, una conocida propiedad que cumplen la mayoría de los metales.
Para entender mejor de que se trata el asunto, recordaremos brevemente qué es el grafeno y cuales son sus principales propiedades, así como en qué consiste la ley de Wiedemann-Franz . Después de estos recordatorios estaremos en mejores condiciones de comentar el resultado de referencia y su trascendencia.
El grafeno y sus propiedades especiales.

El grafeno es una lámina de átomos de carbono dispuestos imaginariamente formando una red hexagonal (como un panal de abejas), con un espesor de un solo átomo (figura 1) . Cada átomo de carbono tiene 4 electrones de valencia. En el grafeno, 3 de estos electrones forman enlaces covalentes fuertes con sus tres vecinos, creando la estructura hexagonal rígida. El cuarto electrón está “deslocalizado”, lo que significa que puede moverse libremente por toda la red, de forma semejante a como lo hacen los electrones de valencia en los metales más comunes como el oro, la plata, el hierro y otros.
Es conocido que en los sólidos, los niveles de energía de los electrones individuales se fusionan para formar “bandas” de energía permitidas, que pueden estar separadas por zonas de energía prohibida. Las dos bandas más importantes son: la Banda de Valencia, que está llena de electrones y la Banda de Conducción que, o bien está vacía, o está parcialmente llena. En este último caso, los electrones son libres de moverse y conducir la electricidad.
Para establecer la estructura de banda de los materiales, los físicos calculan la relación entre la energía de los electrones y la magnitud el vector de ondas asociado a ellos (que está íntimamente relacionado con su momento lineal). En la mayoría de los materiales (como, por ejemplo, el silicio) esa relación es de la forma
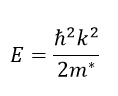
donde ℏ es la constante de Placnk reducida. Esa relación cuadrática es análoga a la que se obtiene en la Mecánica de Newton para una partícula libre de momento lineal p y masa m, o sea E=p^2/2m. De modo que en los materiales convencionales los electrones se pueden considerar como “cuasipartículas” que se mueven en la red cristalina como si tuvieran un momento lineal de magnitud y una masa efectiva.
Esa masa efectiva en general es diferente a la masa del electrón libre, pues tiene incluidos los efectos del potencial periódico de la red cristalina. Este movimiento de los electrones se puede describir como si esas cuasipartículas formaran una especie de líquido, que se conoce como Liquido de Fermi.
Sin embargo, cuando se estudia la relación entre E y k para los electrones moviéndose en la red hexagonal del grafeno los resultados son totalmente diferentes. Aquí aparecen seis puntos especiales en el espacio de momentos (el llamado espacio recíproco) donde la banda de valencia y la banda de conducción se tocan. Estos seis puntos son equivalentes por simetría, pero se pueden agrupar en dos conjuntos independientes de tres. A estos dos puntos inequivalentes se les llama “Puntos de Dirac” (figura 2 a).
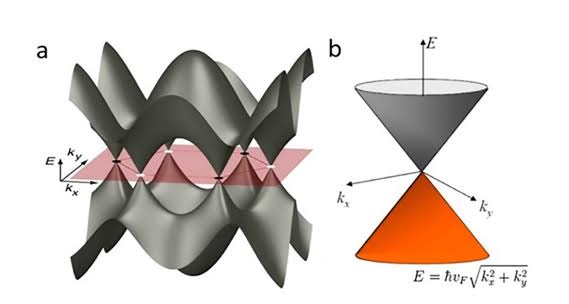
En estos puntos la energía de los electrones es la misma en la banda de valencia que en la banda de conducción. Pero lo mas interesante es que la relación energía-momento alrededor de estos puntos ya no es cuadrática sino lineal y se describe por la ecuación: E=ℏkv_F, donde v_F es la llamada “velocidad de Fermi” (una constante muy grande, aproximadamente 1/300 de la velocidad de la luz). De esta forma, las bandas de energía en la cercanía de los puntos de Dirac adquieren la forma de conos que se han bautizado como “conos de Dirac” (figura 2 b) .
La circunstancia de que la relación entre E y k sea lineal y no cuadrática como en la mayoría de los materiales tiene extraordinarias implicaciones, ya que ese tipo de relación lineal es la que se observa en las partículas relativistas sin masa, como los fotones. Para un fotón se cumple que E=pc donde p es su momento lineal y c es la velocidad de la luz. Por analogía se considera entonces que los electrones en el grafeno se comporten como partículas relativistas sin masa y en ese caso juega un papel al de la velocidad de la luz en los fotones[1].
Por esta razón, los electrones en el grafeno encuentran muy poca resistencia cuando se mueven a través de la red. Esto, combinado con su alta velocidad constante, que es la velocidad de Fermi, conduce a una movilidad electrónica extremadamente alta (100 veces mayor que la del silicio) lo que significa que los electrones pueden viajar distancias largas sin dispersarse.
El comportamiento de los electrones en el grafeno ya no se ajusta al esquema del Líquido de Fermi. Para establecer la diferencia se habla entonces de un Fluido de Dirac. Las propiedades de los fluidos de Dirac se habían establecido teóricamente desde antes del descubrimiento del grafeno, pero poco a poco los resultados experimentales han ido demostrando que este es un modelo muy adecuado para explicar el comportamiento de los electrones en el grafeno, y que este fluido se ajusta muy bien al enfoque denominado de hidrodinámica relativista utilizado para estudiar sistemas cuánticos críticos en los cuales sus componentes se describen por la ecuación relativista de Dirac.
Vale la pena de paso recordar que el grafeno no solo es especial por esas propiedades electrónicas sui generis sino también por otras propiedades físicas excepcionales. De hecho es el material más fino conocido, es 200 veces más resistente que el acero, más duro que el diamante , flexible, transparente e impermeable a los gases.
La Ley de Wiedemann-Franz
Esta ley establece que, para la mayoría de los metales, el cociente entre la conductividad térmica (κ) y la conductividad eléctrica (σ ) es proporcional a la temperatura (T). Es decir, κ/σ = L₀T, donde L₀ es el número de Lorenz, una constante.
Esta ley se cumple cuando las partículas responsables de transportar tanto la carga eléctrica como la energía térmica son las mismas (generalmente electrones) , y cuando las colisiones que dispersan a estos portadores durante su movimiento son elásticas.
Esto se cumple en la mayoría de los metales porque los electrones en ellos se comportan como si fueran un Líquido de Fermi, con las propiedades que hemos descrito mas arriba. En estos materiales, un electrón que choca con una impureza o que interactúa con las vibraciones de la red pierde momento y energía, pero este mecanismo afecta de manera similar al transporte de carga y de calor.
Violación de la ley de Wiedemann-Franz
Aunque esta ley se cumple para un número grande de materiales, no es una ley universal de la Física como pueden ser la Segunda Ley de la Termodinámica o la Ley de Conservación de la Energía. De hecho, se han encontrado desde hace varios años materiales que no la cumplen, lo cual se debe a que en ellos no se satisfacen estrictamente las condiciones de que los portadores de carga se comporten como liquidos de Fermi, ya que aparecen otros mecanismos de interacción que son diferentes para el proceso de conductividad eléctrica y de conducción del calor.
Como hemos explicado más arriba el grafeno se comporta como un Fluido de Dirac y no como un Líquido de Fermi convencional. Esta diferencia fundamental es la causa de la violación de la Ley de Wiedemann-Franz.
Dentro de ello, debemos tener en cuenta que en el grafeno surgen procesos de dispersión de los electrones que se diferencian de los de los metales tradicionales. Por ejemplo, en el grafeno desempeña un papel importante la dispersión por impurezas cargadas (llamada scattering de Coulomb), un mecanismo muy eficiente para frenar la corriente eléctrica, pero menos para frenar el flujo de calor.
Otro elemento es que en el grafeno las interacciones electrón-electrón pueden llevar a un comportamiento colectivo donde el transporte de calor y de carga se “desacoplan” aún más. El calor puede ser transportado por fluctuaciones colectivas (como ondas de densidad o de espín) que no transportan carga neta.
De modo que no es ninguna sorpresa que en el grafeno de viole la ley de Wiedemann-Franz. De hecho , esto se había predicho teóricamente por varios autores y además en los últimos años se han reportado algunos resultados experimentales que corroboraban esta hipótesis. Sin embargo, estos datos hasta ahora eran muy dependientes del dispositivo especifico donde se desarrollaba el experimento y no tenían el grado de generalidad necesario para sustentar la teoría.
El gran valor del trabajo referenciado, realizado por investigadores indios con la participación de científicos de otras nacionalidades, es precisamente que ha establecido el carácter universal de esa violación, respaldada en datos obtenidos experimentalmente en forma muy rigurosa , utilizando grafeno de alta calidad y numerosos dispositivos experimentales diferentes.
Como resultado ellos han reportado lo que han dado en llamar una “violación gigante” de la Ley de Wiedemann-Franz , encontrando que a bajas temperaturas y cerca del punto de Dirac, el número de Lorenz efectivo es 200 veces superior al valor clásico. Además, de estos aspectos, el trabajo incluye otros resultados experimentales que corroboran fehacientemente la validez de considerar el comportamiento de los electrones en el grafeno como un Fluido de Dirac.
Relación del grafeno con el plasma de quarks- gluones
El Fluido de Dirac puede considerarse como un estado de la materia bastante exótico y muy pocos sistemas físicos conocidos lo exhiben. Desde el punto de vista teórico uno de los sistemas que pueden describirse con ese modelo es el llamado “plasma de quarks-gluones” (QGP).
Es conocido que los protones y neutrones no son en realidad partículas elementales, como se creía a mediados del siglo pasado, sino que están constituidos por otras partículas mas simples llamadas “quarks”.
Esos quarks en condiciones normales están confinados dentro de los protones o neutrones, unidos entre sí por otras partículas llamadas “gluones” que actúan como una especie de pegamento para los quarks.
Sin embargo, en condiciones muy extremas, puede lograrse que los quarks y gluones, en lugar de estar confinados en protones y neutrones, se muevan libremente en un medio de gran densidad y temperatura, de altísima energía, que es precisamente el QGP. Al igual que en el grafeno, las quasipartículas en el QGP (quarks y gluones) interactúan fuertemente. El transporte de carga y energía en este medio también puede describirse mediante hidrodinámica relativista y modelarse como un Liquido de Dirac.
Por supuesto, los QGP no existen actualmente en la naturaleza, se cree que este es el estado de la materia existente en los primeros instantes del universo, inmediatamente después del Big Bang.
Desde los años 80 se ha intentado obtener este extraordinario plasma en los grandes aceleradores de partícula del CERN y otros centros de investigación de los países más desarrollados. Se han reportado resultados de su obtención parcial, pero se continúa intensamente su búsqueda pues obtenerlo suficiente tiempo y estudiarlo permitiría completar muchos conocimientos sobre las interacciones fuertes y otros aspectos esenciales de la física actual.
Sin embargo, esos son experimentos extremadamente complejos y muy costosos. De ahí la gran importancia que tiene contar con un sistema relativamente sencillo, como el grafeno, que presenta propiedades que son semejantes a las del QPG. Por supuesto son sistemas diferentes, de hecho el origen de las interacciones es distinto, pero aun así el grafeno puede servir para modelar muchos aspectos de ese interesante y complejo estado de la materia, y ello puede hacerse a partir de experimentos muchos mas sencillos que están al alcance de un laboratorio universitario.
Al medir las propiedades de transporte térmico y eléctrico, la capacidad calorífica, etc., en el grafeno, se están poniendo a prueba las predicciones teóricas sobre cómo se comportaría un Fluido de Dirac en general, incluyendo el de quarks.
¿Es realmente el grafeno el material del siglo?
El descubrimiento del grafeno y de sus sorprendentes propiedades despertó de inmediato un extraordinario interés y muchos colectivos de investigación en todo el mundo empezaron a buscar posibles aplicaciones en diferentes campos. Una muestra de ello fue que solo seis años después de su obtención en el laboratorio, los descubridores del grafeno fueron galardonados con el Premio Nobel de Física, un tiempo inusualmente corto para estos premios.
Muy pronto comenzaron a aparecer resultados prometedores y proptotipos de aplicaciones en la electrónica, el almacenamiento de energía, la purificación de agua, los sensores y la biomedicina. Ello hizo que se le calificara como “el material del siglo” y que no fueran pocos los que vaticinaran una nueva revolución en la electrónica con el grafeno como sustituto del silicio.
Sin embargo, 20 años y algo después de su descubrimiento son relativamente pocas las aplicaciones comerciales del grafeno y la pronosticada revolución no se ha producido. La causa principal de esto ha sido la dificultad de lograr una producción de grafeno en gran escala y con alta calidad.
Las propiedades del grafeno dependen mucho de su grado de pureza y de la presencia de defectos, y ello es bien difícil de lograr. No obstante, hay resultados prometedores en este sentido y se sigue trabajando fuertemente en los métodos de fabricación. Esta circunstancia ha hecho que algunos se decepcionen del grafeno y consideren que realmente no merece el titulo de material del siglo.
En mi opinión la relevancia del grafeno no está solo en las aplicaciones prácticas que puedan desarrollarse mas o menos a corto plazo, sino en la riqueza de propiedades que posee y que lo convierten en un verdadero laboratorio no solo para profundizar en la física de la materia condensada, sino, como hemos visto, que pueden ser muy útiles para comprender propiedades fundamentales de la materia.
Hay un aspecto adicional que es el referido al de las propiedades del grafeno de varias capas. Además del grafeno monocapa, que es al que nos hemos referido hasta ahora en este trabajo, también se consideran como tipos de grafeno ( o como “materia grafénica” si nos apegamos a la nomenclatura de la ISO) aquellos materiales formados por hasta 10 capas de grafeno apiladas .
Es el llamado “Grafeno de Pocas Capas”. Lo interesante es que en los últimos años se vienen descubriendo propiedades interesantísimas en este tipo de grafeno, donde la riqueza física es sorprendente y extraordinaria. Es un tema apasionante donde hay mucha tela por donde cortar, y quizás pueda ser motivo de un comentario posterior.
Por todo ello, mi voto es a favor de seguirlo considerando como material del siglo. Ningún otro material descubierto en este siglo ha tenido tanto impacto científico….no obstante, dejo abierta la pregunta.
[1] Las partículas cuánticas relativistas están descritas por la llamada Ecuación de Dirac, descubierta por el eminente físico de origen británico Paul A.M. Dirac, ganador del premio Nobel de Física en 1933 por sus extraordinarios aportes a la Física Cuántica. Esa es la causa de que los puntos especiales en la red reciproca del grafeno se llamen puntos de Dirac y también que se denominen conos de Dirac a esa forma cónica que adquieren las superficies de energía vs momento alrededor de los puntos de Dirac.

