Del caos al ritmo: la danza molecular que gobierna al mundo

El 5 de septiembre de 1906, en un hotel de una ciudad de Italia Ludwig Boltzmann —el hombre que había visto el orden en el caos— se ahorcó.   Solo una década antes, James Clerk Maxwell —el genio que unificó la electricidad y el magnetismo— había muerto de cáncer abdominal a los 48 años, sin imaginar que su trabajo sobre las velocidades moleculares se convertiría, junto al de Boltzmann, en la piedra angular de la física estadística. 

Ambos habían descubierto algo revolucionario: las moléculas no se mueven al azar, sino siguiendo un patrón oculto. Pero mientras Maxwell murió reconocido, Boltzmann lo hizo en la oscuridad, acosado por las burlas de quienes creían que “los átomos eran solo un truco matemático”. Y es que, aunque el movimiento de una sola partícula puede parecer aleatorio, cuando se observan muchas partículas, se pueden establecer patrones. La distribución de Boltzmann describe esos patrones.

Para entender mejor todo podemos imaginar que el universo es un estadio gigante y las moléculas que están contenidas en él son los deportistas. Esa sería una buena forma de ver al mundo que esos dos científicos descubrieron.  Algunas, las corredoras promedio, tendrían una velocidad similar a la de un avión de combate; luego, las más lentas se moverían al ritmo de simples autos de ciudad y las rápidas,  las que llegan siempre en primer lugar, serían hasta cinco veces más veloces que las balas de un rifle.

¿Pero cómo funciona este ranking de velocidades? Pues la temperatura actuaría como el entrenador principal y cuanto más caliente sea el ambiente más moléculas lograrán entrar al club de deportistas élites. La masa molar, por otro lado, sería como el peso de los zapatos, haciendo que las más ligeras siempre gocen de ventaja.

 Esta analogía nos ayuda a visualizar cómo la temperatura y la masa molar influyen en las velocidades moleculares, pero, ¿cómo se traduce esto en ecuaciones?

Precisamente la función de distribución de las velocidades no es más que un valor de probabilidad , la búsqueda de qué tan probable es que existan moléculas con determinada velocidad. , y en el caso de la energía la probabilidad de encontrarlas con dicha energía.

Es importante aclarar que el término distribución de Boltzmann se reserva para la función de probabilidad de la energía de las partículas, mientras que el término distribución de Maxwell-Boltzmann se guarda para la distribución de probabilidad de la velocidad.

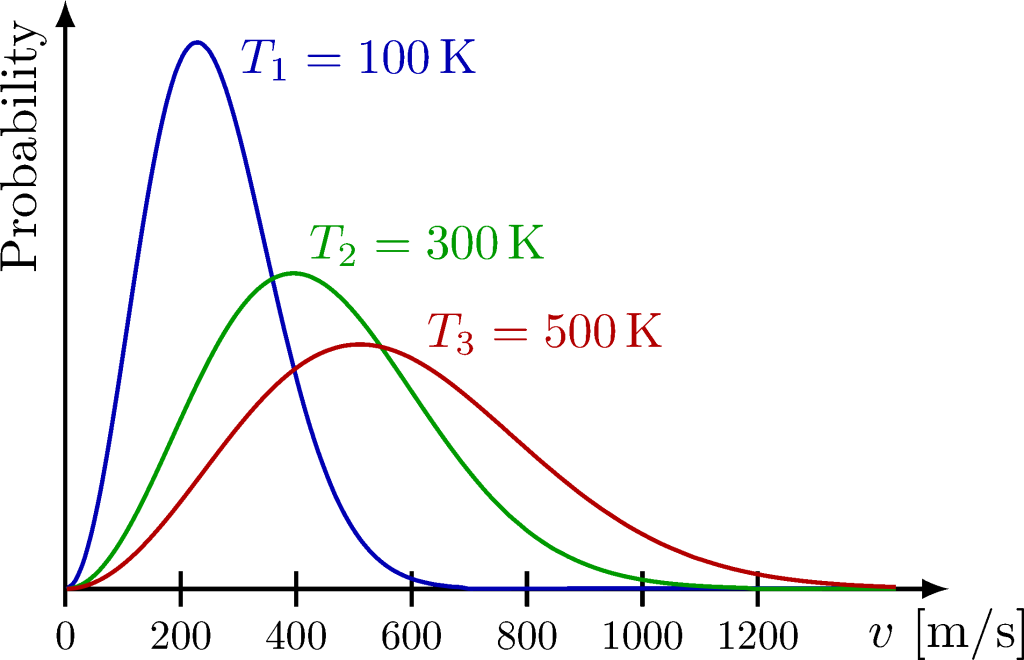
Los valores recopilados normalmente se agrupan en gráficas que tienden a tomar formas de campana, siendo el pico la velocidad más probable.

A temperaturas muy altas, la energía térmica (grado de energía interna contenida en un sistema termodinámico en equilibrio que es proporcional a su temperatura absoluta )  es mucho mayor que la energía cinética típica de las partículas, lo que hace que la distribución se extienda y que más partículas adquieran velocidades altas. Para partículas con masas muy bajas, como electrones, la distribución se vuelve más ancha, permitiendo que alcancen mayores velocidades a una temperatura dada.

Casi simultáneamente a las investigaciones de Maxwell, el físico austriaco Ludwig Boltzmann realizó estudios similares, por ello se la conoce como distribución de Maxwell-Boltzmann,

El lector puede estarse preguntando para este punto de qué forma se visualiza esto en su vida diaria y la respuesta está tan cercana como un ventilador, un frasco de  perfume e incluso los globos que cuelgan en los cumpleaños.

Cuando encendemos un ventilador, sus aspas giran y crean una brisa agradable haciendo más soportable el calor . El secreto científico detrás de esto se encuentra en que el ventilador no baja la temperatura del aire, solo nos ayuda a engañar a nuestro cuerpo. Las gotas de sudor están formadas por moléculas de agua que para evaporarse necesitan robar energía térmica de nuestra piel.

Aquí es donde entra la distribución, ya que todas las moléculas no se mueven de igual forma, las lentas se quedan pegadas a la piel y las más rápidas son las que logran escapar. El ventilador actúa como agente de tráfico y remueve el aire estancado alrededor de nosotros para que a  las moléculas veloces  les sea más fácil escapar y las lentas tengan mayor oportunidad. Esto no se cumple en lugares húmedos porque ya el aire está cargado de moléculas de agua y le es más difícil al sudor evaporarse. Si no existiera esa variación de velocidades todas las moléculas se moverían igual y el ventilador no pudiera “seleccionar” las más rápidas.

En el perfume, las moléculas están diseñadas para ser pequeñas y ligeras (como el alcohol o compuestos aromáticos), por lo que son las ganadoras de la competencia, mientras que, por ejemplo, en el olor a pescado son moléculas grandes y pesadas por lo que el olor parece quedarse pegado eternamente al aire.

El globo de helio es otra evidencia de este fenómeno en acción: sus moléculas ultraligeras (cuatro veces más livianas que las del aire) se mueven a velocidades vertiginosas según la distribución de Maxwell-Boltzmann. Esta rapidez extrema hace que choquen con más fuerza y frecuencia contra las paredes del globo, creando una presión interna mayor que la del aire circundante y generando el empuje ascendente. Las moléculas más veloces  son las primeras en escapar lentamente a través del material del globo, lo que explica por qué pierde flotabilidad con el tiempo.

Pero ¿por qué es tan importante? Resulta  que estos permiten modelar el comportamiento de la atmósfera planetaria y el viento solar, diseñar sensores de gases y membranas de filtrado y otras muchas aplicaciones en el sector nuclear para lograr reacciones controladas.

Así que la próxima vez que sientas la brisa de un ventilador, percibas el aroma de un perfume u observes un globo de helio elevándose, recuerda: estás presenciando el legado invisible de Boltzmann y Maxwell. Su trabajo no solo reveló el orden oculto en el caos molecular, sino que sentó las bases de tecnologías que hoy dan forma a nuestro mundo, desde la predicción del clima hasta la energía nuclear. Aunque Boltzmann no vivió para ver su triunfo, su distribución sigue viva en cada partícula del universo, demostrando que incluso en la aparente aleatoriedad, la ciencia encuentra patrones que nos acercan a comprender los misterios más profundos de la naturaleza.

Bibliografía : 

- Estudiando. (2007, 7 de abril ). Distribución de Boltzmann: definición, ecuación y curva de temperatura. https://estudyando.com/distribucion-de-boltzmann-definicion-ecuacion-y-curva-de-temperatura/

- Wikipedia. (s.f.). Distribución de Boltzmann. https://es.wikipedia.org/wiki/Distribuci%C3%B3n_de_Boltzmann

- Wikipedia. (s.f.). Ludwig Boltzmann. https://es.wikipedia.org/wiki/Ludwig_Boltzmann