Por Lic. Cristina Díaz Faloh y Dr. Roberto Mulet/Imagen: tomada de La Razón
El 8 de octubre se anunció que el Premio Nobel de Física del 2024 sería para John Hopfield y Geoffrey Hinton por “descubrimientos fundacionales e invenciones que permiten el aprendizaje automático con redes neuronales artificiales”. En el mundo que vivimos no creo que a nadie le cause asombro que quienes contribuyan al desarrollo de la inteligencia artificial se les concedan reconocimientos, pero ¿por qué el Nobel de…Física? Aquí intentaremos explicar esta cuestión.
John Hopfield ha tenido una carrera extraordinaria en el ámbito de la Física. Obtuvo su licenciatura en la especialidad en Swarthmore College en 1954 y completó su doctorado en la Universidad de Cornell en 1958. Comenzó su carrera en los Laboratorios Bell de AT&T, donde se centró en la física del estado sólido y antes de trasladarse al ámbito académico introdujo en Física el concepto de Polaritón. Fue profesor en la Universidad de Princeton y actualmente lo es en el Instituto Tecnológico de California (Caltech), donde también contribuyó significativamente a los campos de la química y la biología.
Sin embargo, fue a principios de la década de 1980 cuando comenzó a trabajar en el tema que le valdría el Premio Nobel de Física. Dos de sus artículos presentaron una red artificial que podía funcionar como “memoria” y que posteriormente se conocería como la Red de Hopfield, en su honor.
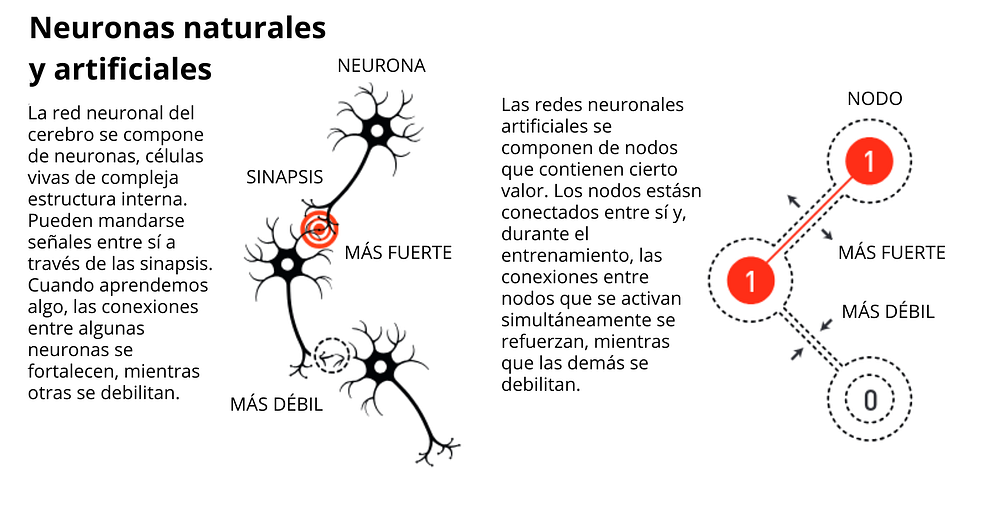
Este modelo consiste en una red de neuronas artificiales, inspirada en el funcionamiento de las neuronas en el cerebro humano. Nuestro cerebro puede entenderse como una extensa red de neuronas que se comunican entre sí mediante sinapsis. Al aprender algo, las conexiones entre algunas neuronas se fortalecen, mientras que otras se debilitan. De manera análoga, la red de Hopfield es un conjunto de nodos que pueden tomar distintos valores y están completamente interconectados. Durante el entrenamiento, las conexiones entre nodos que se activan simultáneamente se refuerzan, mientras que las demás se debilitan.
La red de Hopfield se entrena para recordar ciertos patrones, como, por ejemplo, los píxeles de una imagen en blanco y negro de un gato. Durante el entrenamiento, al sistema se le “muestra” la imagen que debe recordar. En este contexto, los nodos de la red representan cada uno de los píxeles de la imagen, y cada conexión entre un par de nodos recibe un valor mayor cuanto más similares son los valores de ambos nodos.
Esto puede interpretarse como que, durante el proceso de ajuste de las conexiones, el modelo asigna una cierta “energía” a cada configuración posible de píxeles. Esta función de energía depende tanto de los nodos como de las conexiones de la red y está inspirada en la energía de sistemas de partículas bien conocidos en la Física.
Luego del entrenamiento, la red habrá construido un “paisaje” de energía en el que los máximos representan configuraciones de píxeles muy diferentes a las de las imágenes de entrenamiento — como una imagen completamente en negro o en blanco — , mientras que el mínimo corresponde al patrón deseado.
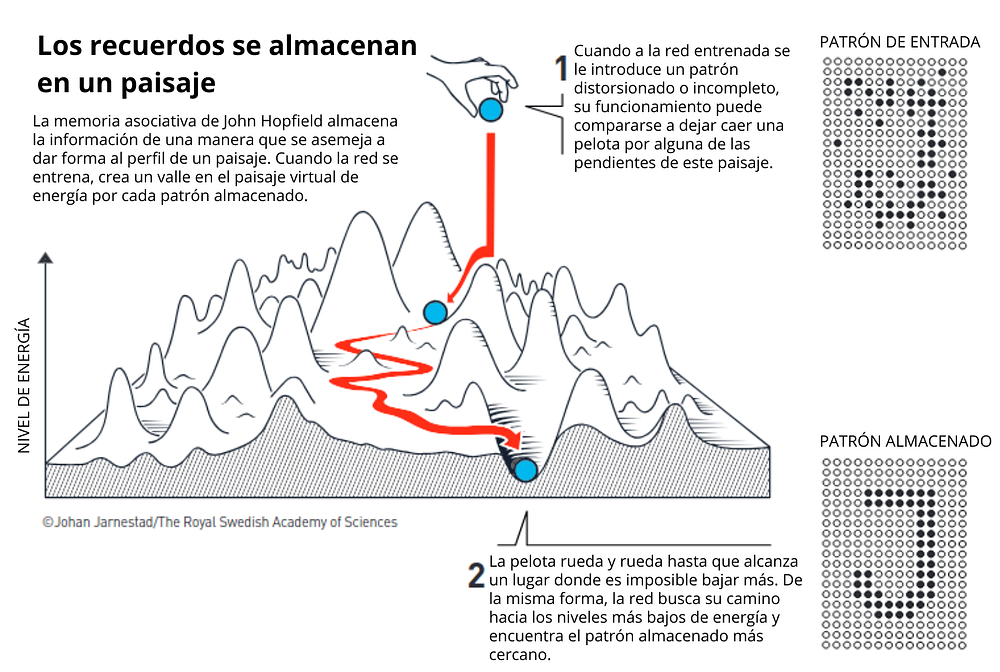
Una vez ajustadas todas las conexiones, si al modelo se le presenta una imagen distorsionada, será capaz de explorar su memoria, es decir, su paisaje de energía, y desplazarse gradualmente hacia el mínimo, ajustando la imagen propuesta hasta recuperar lo que la red ha aprendido: la imagen del gato. Las redes de Hopfield, aunque de uso limitado, demostraron la capacidad de las redes neuronales artificiales para almacenar y recuperar patrones de información, sentando un precedente para el trabajo que Hinton desarrollaría más adelante.
Geoffrey Hinton estudió psicología experimental antes de obtener su doctorado en Inteligencia Artificial (IA) en 1978, en una época en que las computadoras personales eran poco comunes y no existían las laptops. Solo unos años después de su doctorado, analizó las Redes de Hopfield y modificó su dinámica. De esta forma desarrolló un nuevo tipo de red neuronal llamado Máquina de Boltzmann, que tiene la capacidad de aprender patrones complejos en conjuntos de datos. A diferencia de las redes de Hopfield, que solo pueden almacenar patrones específicos, la Máquina de Boltzmann puede identificar características comunes y generales en los datos a través de un método probabilístico.
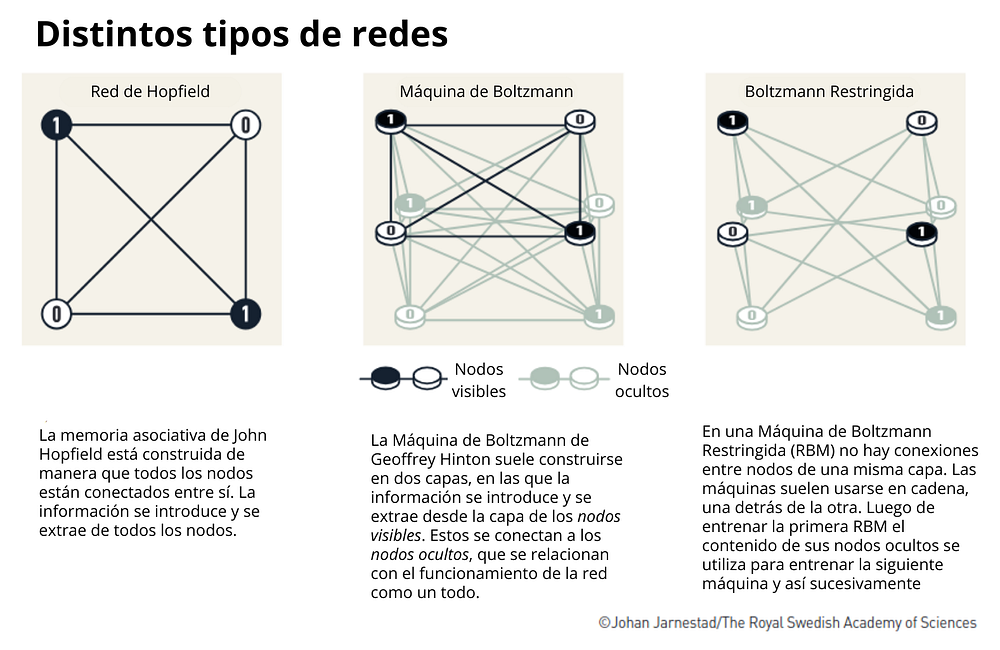
La Máquina de Boltzmann se compone de nodos visibles y nodos ocultos. Los nodos visibles representan los datos que queremos que la red aprenda, mientras que los nodos ocultos permiten a la máquina captar relaciones más profundas entre los datos, modelando patrones más complejos. Estos nodos ocultos son importantes porque ayudan a que la red “generalice” y no solo memorice ejemplos específicos.
Para entrenar la Máquina de Boltzmann, se le muestran ejemplos de datos que tienen una alta probabilidad de aparecer en el conjunto que deseamos que la red aprenda. Durante este proceso, la máquina ajusta sus conexiones internas para que, cuando se le presenten datos similares a los ejemplos, pueda identificarlos como parte de un mismo tipo de patrón. Esta capacidad le permite clasificar datos y también generar nuevas muestras similares a las que ya ha aprendido.
La Máquina de Boltzmann también explota la idea del “paisaje de energía” durante el entrenamiento y al generar nuevos datos. Siguiendo el ejemplo anterior, una tarea típica para esta máquina sería no ya recordar una imagen específica de un gato, sino aprender el concepto abstracto de “gato” tras observar múltiples imágenes de estos animales. Esto significa que, una vez entrenada, la red es capaz de generalizar, generando nuevas imágenes que, aunque sean diferentes de todas las de entrenamiento, aún se reconozcan como gatos.
Las Máquinas de Boltzmann no son muy utilizadas en la práctica, pues entrenarlas es por lo general muy costoso computacionalmente. Sin embargo, una variante modificada conocida como Máquina de Boltzmann Restringida (RBM por sus siglas en inglés) se convirtió en una herramienta versátil que inspiró la creación de máquinas más complejas en el campo de la inteligencia artificial. A diferencia de las máquinas de Hopfield y Boltzmann, que son redes completamente conectadas, las RBMs están compuestas por dos capas consecutivas. Esta estructura es fundamental para lo que hoy conocemos como aprendizaje profundo, que implica el uso de múltiples capas conectadas.
Geoffrey Hinton fue pionero en el avance de la inteligencia artificial al demostrar que las redes neuronales pueden aprender a partir de datos. Continuó desarrollando esta idea a través de publicaciones influyentes sobre backpropagation — el proceso que utilizan los sistemas de inteligencia artificial modernos — y redes neuronales convolucionales, logrando transformar conceptos de la ciencia de los años ochenta en aplicaciones prácticas contemporáneas.
Las redes neuronales artificiales (ANN por sus siglas en inglés) se han convertido en herramientas cruciales para la física moderna, facilitando avances en áreas tan diversas como la ciencia de materiales, el clima, la física de partículas y la astrofísica.
En ciencia de materiales, por ejemplo, las ANN ayudan a resolver la compleja ecuación de Schrödinger para calcular propiedades fundamentales, como los gaps de banda y comportamientos emergentes, reduciendo significativamente los recursos computacionales sin perder precisión. Del mismo modo, en modelos climáticos, las ANN mejoran la resolución de las simulaciones a partir de grandes volúmenes de datos sin aumentar el poder computacional necesario.
En física de partículas, las ANN fueron claves para el descubrimiento del bosón de Higgs, mientras que en astrofísica han permitido desde clasificar espectros hasta generar imágenes inéditas del agujero negro en el centro de la Vía Láctea y un “mapa” de neutrinos de la galaxia. La versatilidad de las ANN sigue ampliando los horizontes de la física, facilitando el descubrimiento y la exploración científica en niveles sin precedentes.
Más allá de un reconocimiento a pioneros en la Física, este Premio Nobel representa un mensaje claro: la Física debe entenderse en un sentido amplio, que trasciende sus fronteras convencionales. No se reduce al estudio de los cuerpos en movimiento, o de los campos electromagnéticos en la naturaleza. Tampoco se reduce al estudio de la interacción entre ellos. Hoy la Física busca nuevas leyes universales en la Biología, la Economía, las Finanzas, las Ciencias de la Computación, y la Sociedad, y lo hace llevando a estas ramas del conocimiento herramientas, ideas y conceptos que ampliaron nuestra comprensión sobre la interacción de la materia con los campos.

