Del determinismo clásico a la indeterminación cuántica

Una costumbre muy arraigada en los seres humanos es celebrar los aniversarios de acontecimientos que, de una forma u otra, han marcado el desarrollo de sus vidas. Usualmente, esas celebraciones incluyen fiestas, reuniones, regalos…  Pero si ese aniversario corresponde al nacimiento de una rama de la ciencia que le abrió las puertas a un mundo infinitamente rico en manifestaciones, las cuales han desempeñado y lo seguirán haciendo un papel fundamental en el desarrollo de la humanidad, la celebración debe ser muy especial.

Nos estamos refiriendo al centenario del trabajo donde se estableció, por primera vez, una estructura matemática coherente de la Mecánica Cuántica. Ese texto, publicado en julio de 1925, lleva la firma del reconocido físico alemán Werner Heisenberg.

Mucho se puede decir en relación con el desarrollo y aplicaciones de la Mecánica Cuántica en sus cien años de existencia. Eso es importante y debe hacerse, pero también lo es conocer las circunstancias que dieron lugar a su aparición. Ese conocimiento permitiría, entre otras cosas, valorar apropiadamente el desarrollo científico y tecnológico que hoy muestra la humanidad. Con ese objetivo en mente trataremos de explicar cómo las ideas físicas se fueron sucediendo en el tiempo hasta dar lugar al nacimiento de la Mecánica Cuántica.

Podemos empezar con el libro publicado por el físico inglés Isaac Newton en 1687, Philosophiae Naturalis Principia Mathematicas, donde aparecen por primera vez las tres leyes fundamentales de la Mecánica Clásica. Leyes que no aparecieron de un día para otro; surgieron del análisis de trabajos científicos previos realizados por pensadores talentosos, como el italiano Galileo Galilei, el francés Blaise Pascal, el alemán Johann Kepler, etc.

Con la aparición de esas leyes se contó con una teoría única que explicaba satisfactoriamente los fenómenos que se conocían hasta entonces, los macroscópicos.

El desarrollo subsiguiente estuvo marcado por la tendencia de los investigadores a enmarcar, dentro de la mecánica Newtoniana, los diferentes fenómenos que fueron apareciendo, incluyendo los térmicos, ópticos y electromagnéticos. Lo logrado con esa filosofía sugería que esa teoría era infalible y todo estaba predeterminado, regido por lo que se conoce con el nombre de determinismo mecánico.

Todo marchaba sin serias dificultades hasta finales del siglo XIX, cuando aparecieron fenómenos que no aceptaban ser enmarcados dentro del esquema clásico, formado por la Mecánica y las demás ramas de la Física que surgieron posteriormente, tales como la Termodinámica, la Óptica Física y la Geométrica, la Electrodinámica, etc.

Entre esos fenómenos destacan el espectro de radiación del cuerpo negro, el efecto fotoeléctrico, los espectros de absorción y emisión de radiación electromagnética (luz) por la materia, especialmente los de rayas, y la radioactividad. La física entró en un periodo de crisis que era necesario encarar con ideas nuevas, revolucionarias, y así fue.

El cuerpo negro y los cuantos de energía

Las primeras ideas aparecieron en el estudio del espectro de radiación del cuerpo negro, el cual, como su nombre indica, absorbe toda la luz que incide sobre él. Además, bajo agitación térmica, es un emisor de radiaciones, cuyas intensidades son más fuertes que las de cualquier otra sustancia.

Ciertamente, para finales del siglo XIX se conocía que la densidad de energía de la radiación del cuerpo negro, para una temperatura , exhibe una dependencia con la frecuencia como la mostrada en la Figura 1. A pesar de que ese comportamiento es relativamente sencillo, las leyes clásicas no alcanzaron para explicarlo. En efecto, los estudios clásicos condujeron a las fórmulas de Rayleigh-Jeans y Wien, las cuales solo permiten explicar los comportamientos asintóticos de dicho espectro para bajas y altas frecuencias, respectivamente, como se señala en esa misma figura.

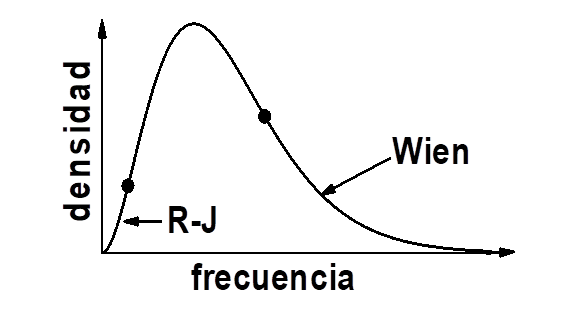
Esos resultados indicaron que la explicación de dicho espectro había que buscarla fuera de los límites clásicos, y eso fue lo que hizo el físico alemán Max Planck el 14 de diciembre de 1900 en un informe presentado ante la Sociedad Alemana de Física.

Planck planteó específicamente que, para explicar ese espectro, es necesario aceptar que el intercambio de energía entre el campo de radiación y la materia no se llevaba a cabo de forma continua, como se suponía hasta entonces, sino en cantidades finitas o cuantos de luz. Planteó, además, que la energía de cada cuanto estaba relacionada con la frecuencia  asociada con el color de la luz considerada por la relación: E=hν=ħω (1), donde h es la famosa constante de Planck ħ=h/2π y ω=2πν es la frecuencia angular.

A pesar de que la teoría de Planck explicaba coherentemente el espectro de radiación del cuerpo negro, la comunidad de físicos de la época no la acogió con el entusiasmo que merecía. Eso se debió, tal vez, a que la explicación dada utilizaba argumentos que contradecían conceptos clásicos ampliamente aceptados.

El efecto fotoeléctrico y la naturaleza corpuscular de la luz

Las ideas cuánticas de Planck permanecieron en silencio durante varios años, hasta que en 1905 Albert Einstein las adoptó para explicar el efecto fotoeléctrico.

Este fenómeno, descubierto por el físico alemán Heinrich Hertz en 1887, consiste en la emisión de electrones por un metal cuando sobre su superficie incide luz con frecuencia  mayor que cierta frecuencia , la cual depende del material considerado.

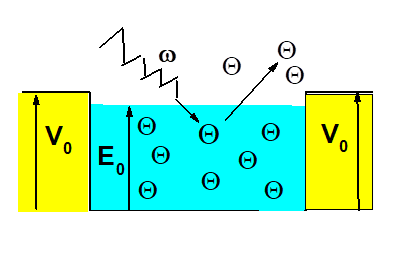
Una ilustración sencilla de ese efecto se muestra en la Figura 2, donde el metal se representa por una región (verde) rodeada por una barrera de potencial (amarilla) de altura V₀ impenetrable a los electrones. Como se ve, para extraer un electrón del metal, se le debe transferir una energía que sea mayor que (V₀ – E₀) , la cual debe ser cedida por la luz incidente, donde  es la energía máxima que un electrón puede tener en el metal.

 Los resultados anteriores indican que entre la frecuencia umbral  y la energía mínima de excitación (V₀ – E₀) debe existir una cierta relación, la cual es imposible justificar utilizando la teoría ondulatoria de la luz. Es decir, la explicación del efecto fotoeléctrico hay que buscarla fuera de esa teoría.

Eso fue lo que hizo Einstein en 1905 cuando adoptó las ideas cuánticas de Planck y planteó que los cuantos no solo se manifiestan en el intercambio de energía entre la materia y la luz, sino que son partes integrantes del campo de radiación; es decir, la luz está formada por corpúsculos. Esa propuesta permitió explicar el efecto fotoeléctrico con relativa facilidad, pues cuando un cuanto con energía ħω –con ω>ω₀ – incide sobre el metal, un electrón cualquiera puede absorberlo íntegramente y abandonar el material.     

Esa explicación conduce a una situación paradójica desde un punto de vista clásico, pues con la radiación se observan otros fenómenos, tales como la difracción e interferencia, que solo pueden explicarse sobre la base de que esta se comporta como onda. Lo paradójico radica en que, si un sistema clásico se comporta como onda, jamás podrá comportarse como partícula y viceversa, son excluyentes.

Espectros ópticos atómicos. El átomo de Bohr

Por otro lado, a finales del siglo XIX se conocía que un cuerpo, cualquiera que sea su estado de agregación, puede absorber y emitir luz bajo determinadas condiciones, y los responsables de ejecutar esos procesos son sus partes más pequeñas, especialmente los átomos. Se conocía, además, que cada uno de ellos poseía un espectro característico, formado por un conjunto de líneas espectrales bien definidas, como se muestra en la Figura 3 para el átomo de hidrogeno. Pero si en aquella época no se sabía exactamente lo que era un átomo, ¿cuáles eran entonces los mecanismos físicos que daban lugar a esos espectros?

La respuesta a esa pregunta no fue inmediata, comenzó a elaborarse después del descubrimiento del electrón por el físico ingés J. J. Thomson en 1897, y aceptarse que ellos son parte integrante de los átomos. Esto último y el hecho de que cada átomo, bajo condiciones normales, tenía que ser eléctricamente neutro, implica la existencia de una distribución de carga positiva dentro de él que compense la carga negativa de los electrones. Comenzó entonces el interés por conocer la estructura interna de los átomos.

Fue ese el contexto donde aparecieron varios modelos de átomos, pero solo uno prevaleció, el propuesto por el físico inglés Ernest Rutherford en 1911, después de estudiar la dispersión de partículas con carga eléctrica positiva (partículas alfa) por láminas delgadas de diferentes materiales. En ese modelo la carga eléctrica positiva del átomo se concentra en una pequeña región del especio, llamada núcleo, y los electrones giran en su alrededor.

Es necesario puntualizar que el átomo de Rutherford viola leyes fundamentales de la física clásica, pero prevaleció después que en 1913 el físico danés Niels Bohr lo combinó con las ideas cuánticas de Planck y Einstein para explicar con éxito el espectro de absorción y emisión de luz por el átomo de hidrógeno.

 Bohr no renunció completamente a las leyes clásicas, solo introdujo algunas modificaciones que permitiesen explicar satisfactoriamente los resultados experimentales que se conocían en relación con los espectros ópticos atómicos.  Con esas modificaciones no solo consiguió explicar las propiedades de los espectros de absorción y emisión del átomo de hidrógeno conocidas hasta entonces, sino que predijo otras que posteriormente fueron encontradas experimentalmente.

 A pesar de estos logros, la teoría de Bohr tropezó con serias dificultades que, en definitiva, condujeron a la necesidad de buscar una teoría más completa. La crisis continuaba, pero los resultados de Bohr indicaban que el camino correcto era el trazado por las ideas cuánticas.

El efecto Compton y el comportamiento dual del campo de radiación

Diez años después, en 1923, el físico estadounidense  Arthur Compton estudió experimentalmente la dispersión de un haz de radiación monocromática (rayos x) por electrones libres. En ese experimento, mostrado en la Figura 4, se encontró que la frecuencia de la radiación dispersada ωd depende de la dirección de dispersión y es menor que la frecuencia de la incidente ω.

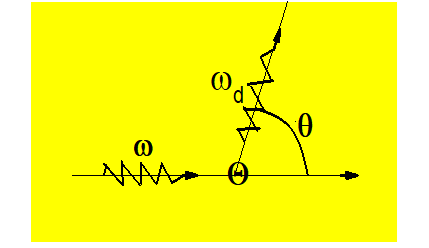
 Así, si aún existían dudas acerca del comportamiento corpuscular del campo de radiación, estos resultados las despejaron. En consecuencia, ese campo exhibe un comportamiento dual: en algunos fenómenos se comporta como onda, difracción e interferencia, y en otros como partícula, efecto fotoeléctrico y efecto Compton.

 Etapa final de la crisis

Así, desde 1900 hasta 1923 la teoría de los cuantos fue ganando terreno y desarrollándose hasta el punto donde su aceptación era ya inevitable. Esta afirmación está avalada por el hecho que su creador, Max Planck, fue galardonado en el 1918 con el Premio Nobel de Física. 

Este fue el planteamiento que catalizó la salida de la crisis, pues poco tiempo después aparecieron los dos trabajos teóricos que contienen la estructura matemática de la Mecánica Cuántica. En uno de ellos se formula la mecánica matricial de Heisenberg, cuyo centenario se celebra este 2025, y en el segundo aparece la mecánica ondulatoria de Schrödinger, que celebrará su centenario un año después.

La veracidad de las ideas de De Broglie fue confirmada por los experimentos de Davisson-Germer en 1027 y Thompson hijo en 1928. En efecto, esos investigadores estudiaron la dispersión de electrones por estructuras cristalinas y observaron un patrón de difracción similar al que se observa con la luz, demostrándose así el comportamiento ondulatorio de los electrones. Estudios similares llevados a cabo con otras partículas, tales como protones, neutrones, átomos, etc., demuestran que cualquier micropartícula exhibe un comportamiento dual. Con estos resultados, la crisis llegó a su fin.

Así, en 1928, la mecánica cuántica es ya una teoría bien establecida, lista para ser utilizada en diferentes escenarios. Es la rama de la física que le abrió las puertas del micromundo al ser humano, un mundo que, como no puede ser percibido directamente con nuestros órganos sensoriales, se necesita un sistema intermedio que traduzca su lenguaje al del macromundo. El funcionamiento de ese sistema debe regirse, por supuesto, por las leyes clásicas. Debe agregarse que en los diferentes estudios, la mecánica ondulatoria de Schrodinger es más utilizada que la mecánica matricial de Heisenberg. Esto es debido a que la primera es conceptualmente más sencilla e intuitiva que la segunda. A pesar de esa diferencia, ambas son equivalentes.

Ese campo también caracteriza sus propiedades corpusculares, pues su módulo al cuadrado, según propuso el físico alemán Max Born en 1926, determina la probabilidad de localizarla espacialmente. De acuerdo con esto, las partículas cuánticas se comportan estadísticamente y, por tanto, no siguen trayectorias bien definidas, como ocurre con las partículas clásicas, es decir, el determinismo mecánico es sustituido por la descripción probabilística o indeterminación cuántica.

Aplicaciones

Las primeras aplicaciones de la mecánica cuántica fueron dirigidas al estudio de átomos, moléculas y sólidos, que condujeron a una descripción excelente de la dinámica de los electrones en esos sistemas.

En átomos, se obtuvieron resultados que explicaron las propiedades conocidas del átomo de hidrógeno y se establecieron métodos que permiten estudiar de forma sistemática las características de átomos con muchos electrones. Algo similar ocurrió en el estudio de las moléculas, pues los métodos mecano-cuánticos utilizados condujeron a la aparición de nuevos conceptos, tales como enlaces covalentes, estados híbridos, etc.

Cuando la mecánica ondulatoria se utilizó para estudiar los sólidos, que son estructuras extremadamente rígidas, formadas por una enorme cantidad de átomos enlazados entre sí por determinados tipos de fuerzas, se obtuvieron resultados que merecen un párrafo aparte.

Sí, porque entre los sólidos estudiados se encontraban los semiconductores, que resultaron ser los materiales apropiados para el desarrollo de la Electrónica Moderna. Esa que, desde mediado del siglo XX a la fecha, ha dado lugar a la revolución tecnológica que ha jugado un rol fundamental en casi todos los aspectos de nuestra vida diaria. Ciertamente, un semiconductor es una substancia cristalina intermedia entre conductora y aislante, que se utiliza para fabricar dispositivos electrónicos de precisión, tales como diodos, celdas solares, transistores, etc.

 La creación del primer transistor en 1947 por J. Bardeen, W. Brattain y W. Shockley marcó el inicio de dicha revolución, pues con ese dispositivo se consiguió controlar, amplificar y generar señales electrónicas. Debido a esas propiedades, los transistores gobiernan las operaciones de prácticamente todos los dispositivos electrónicos modernos, como computadoras, televisores, teléfonos celulares, etc.  

En otras aplicaciones de la mecánica cuántica se estudiaron los núcleos atómicos y diferentes sistemas electrónicos en presencia de campos externos, especialmente de la radiación electromagnética (luz). Esto último dio lugar al desarrollo del láser, un dispositivo cuyas aplicaciones en diferentes campos: la medicina, la informática, etc., etc., etc., son bien conocidas. Se desplegaron, además, importantes ramas, como la información cuántica y la computación cuántica, las cuales están muy relacionadas y son, actualmente, intensamente investigadas debido a la importancia práctica de ambos campos.      

No podemos finalizar sin dedicar unas palabras a la computación cuántica, pues, como es ampliamente reconocido, es una herramienta que promete revolucionar el desarrollo del mundo de las tecnologías. Esta afirmación se puede entender utilizando los siguientes argumentos. En cualquier dispositivo digital, la unidad básica (mínima) de información es el bit (acrónimo de las palabras inglesas binary digit), el cual se acostumbra a representar con cualquiera de los dígitos 0 y 1 del sistema numérico binario. Esos dígitos representan, en general, dos estados diferentes, tales como verdadero o falso, encendido o apagado, etc., y si a uno de ellos se le asocia el dígito 0, al otro le corresponde el 1.

Ahora bien, si se tiene en cuenta que los bits se usan para almacenar y transportar información en los computadores, ¿qué diferencia existe entre el bit clásico y el bit cuántico o qubit, que son los que utilizan las computadoras digitales actuales y cuánticas, respectivamente?

La diferencia fundamental es que el bit clásico solo puede almacenar un estado, el 0 o el 1, mientras que el qubit puede almacenar ambos valores simultáneamente. Esto último es debido al hecho de que como la Mecánica Cuántica es una teoría estadística, los estados asociados con los dígitos 0 y 1 tienen, en cada instante de tiempo, ciertas probabilidades de ocurrencia. Eso significa que una computadora cuántica debe funcionar como muchas clásicas en paralelo, es decir, la cantidad de operaciones que la cuántica puede realizar en la unidad de tiempo es enorme comparada con la clásica.

Eso último justifica los grandes apoyos financieros que han tenido los proyectos destinados a la construcción de computadores cuánticos, y mucho se ha avanzado en ese sentido, incluyendo la fabricación de ordenadores cuánticos aceptables. Pero aún restan diferentes problemas tecnológicos por resolver, especialmente los relacionados con el hecho de que los estados cuánticos son afectados por su entorno, lo cual puede conducir a la pérdida de la información codificada en los bits cuánticos.